
One of the things which I found confusing at first with options, is the fact that lots of the folks trading them, don’t really have a view about whether the spot price will go up and down. They are basically trading the volatility parameter from options pricing models (Emanuel Derman explains the point about trading parameter much better than me here and also here).
One of the most common volatility trading strategies is selling volatility to collect the volatility risk premium. The rationale is that generally volatility used to price the option ends up being higher than the future realized volatility. This differential is known as the volatility risk premium. Typically, this involves selling a straddle. If the price doesn’t move that much, happy days, and you pick up the option premium! The problem is when you have large directional moves, you’ll be subject to large drawdowns… But what about delta hedging? If we’re short a straddle, delta hedging would involve buying spot as it climbs higher, and conversely selling spot if it goes lower. So at least for large directional moves (admittedly with slippage), we’d be able to limit our losses somewhat.
In order to test this idea on some real data, I’ve done an FX options backtest. It can be extremely fiddly to do FX options backtests. First you need to download all the market data. Then you have to create a total returns time series, repricing the options at every point, working out expiry dates and so on. Then you need to work out a trading filter etc.
To make things much easier, I’ll be using my open source Python finmarketpy library (get it from GitHub) for selling short dated straddles in EURUSD and USDJPY, which are repeatedly rolled at expiry. I’ve included transaction costs since 2007 and I’ve reported monthly P&L below. Finmarketpy lets you backtest options strategies with a couple of lines of code, and underneath it does all the option pricing using FinancePy and I’ve written a large amount of code to handle the backtest itself. By default, it downloads FX spot, depo, forwards, volatility surface data etc. from Bloomberg (subscription required), but you can substitute this data from other sources. The FX options functionality is still very much a work in progress in finmarketpy and I’m still ironing out the bugs, so any feedback is appreciated!
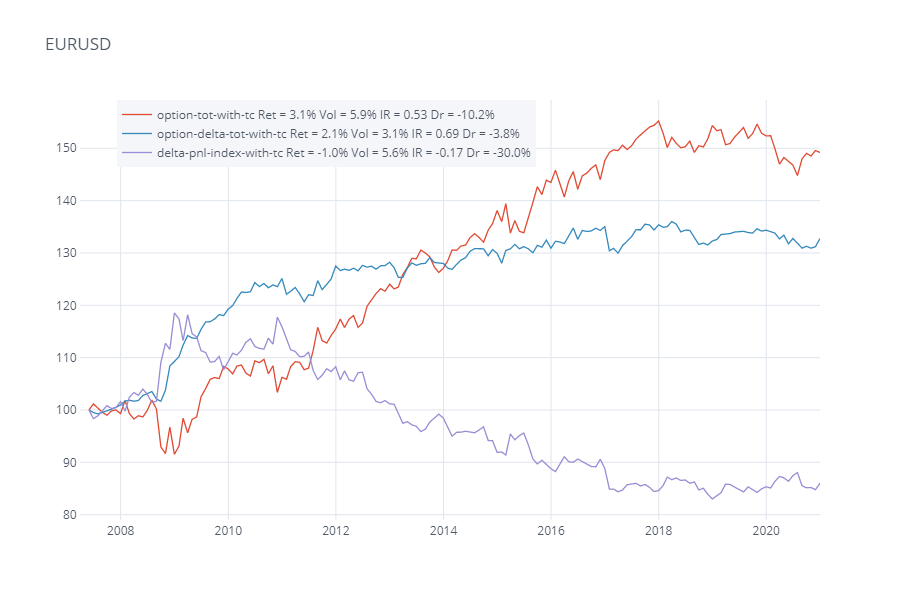
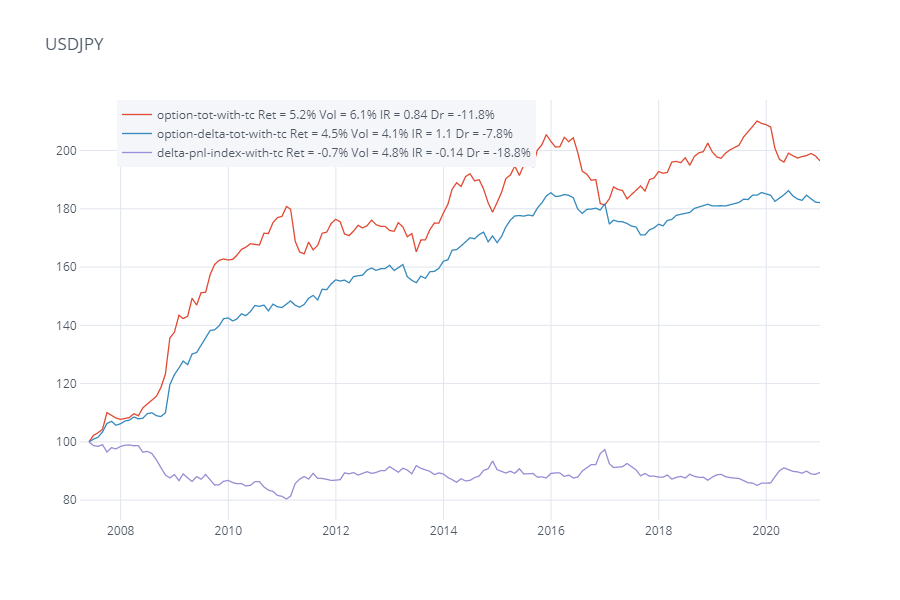
The red lines show the P&L only of selling straddles in each pair, the purple line shows the P&L of delta hedging spot, whilst the blue line shows a portfolio of both. We note the EURUSD and USDJPY portfolios have largely been profitable during the history, although admittedly in recent years it’s mostly been sideways, which suggests that the risk premium isn’t as large as it used to be.
Even though the delta hedging P&L was negative in both instances (in purple), the risk adjusted returns for the portfolios (in blue) were actually higher compared to purely option selling (in blue). During periods where there were big drawdowns for option selling such as during March 2020 for both pairs, delta hedging P&L was positive. Another example of this was seen in Autumn 2008 for EURUSD. So adding delta hedging improves risk adjusted returns and reduces drawdowns in these instances.
Does that mean we should blindly sell volatility all the time? Well, no! For one, it can be the case that in other currency pairs the results might be so good (GBPUSD and Brexit anyone??). Furthermore, there are instances where delta hedging can be very painful, for example, if we’re short vol, and spot keeps going back and forth across the strike, then we’ll end up repeatedly buying high and selling low, and that’s where we can face large drawdowns too. Transaction costs can also mount up even more in less liquid currency pairs, from delta hedging (as well as from selling options).
A few days ago, I posted a similar thread on Twitter, albeit for a more selective sell vol trading rule in USDJPY, and I got a lot of interesting feedback. In particular, @VolQuant noted that your optimal hedging strategy will depend on several factors, such as the vol regime, and if spot is trending. Furthermore, it also depends on other options in your trading book (given that you’d for example aggregate your delta, gamma exposures etc.). It’s also the case that you might have different objectives. Above, I’ve shown that on a risk adjusted basis, delta hedging has helped historically if you look at risk adjusted returns/information ratio. @VolQuant made the point that some traders might prefer reducing the variance of their P&L, whilst others might want to maximize risk adjusted returns etc. All this will impact how you consider how you delta hedge, in terms of the frequency, amount you do etc. There’s an interesting note from @ArturSepp looking at delta hedging P&L in more detail, deriving the formula for relating delta hedging P&L to the differential between implied and realized variance (the risk premium).
Furthermore, in my example, we are systematically selling volatility. Hence, as soon as one contract expires you are selling another one. We might want to think about active trading rules that only sell options when certain criteria are met, rather than doing it on a systematic basis like in my toy example. We should also consider active rules which might buy options as well. Ok, I admit getting a decent vol trading filter is probably where the “secret sauce” is (although, I don’t really believe in secret sauce, when it comes to markets). I have worked on a number of filters in the past. It is an area where I’ll be researching (although I probably won’t be able to publish all of this research!). There’s all sorts of other details that impact the P&L too, such as the tenor of the option, are we trading across the curve, the type of option too, frankly too many to list exhaustively here!
Ultimately, selling options is always going to be subject to some level of drawdowns, however, delta hedging can help at least to mitigate some of these historically. If you have any ideas, on ways to improve upon the P&L of my charts, have a play around with finmarketpy!